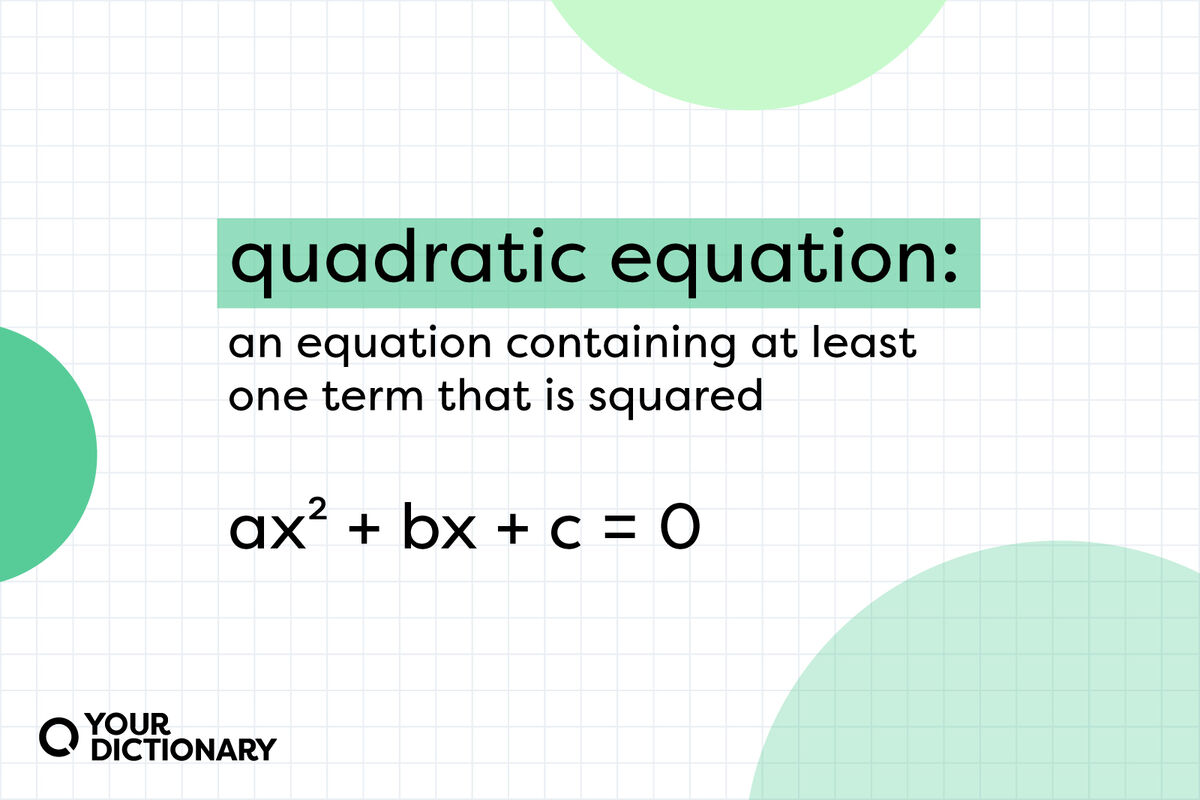
What is a quadratic equation? A quadratic equation is an equation of the second degree, meaning it contains at least one term that is squared. The standard form is ax² + bx + c = 0 with a, b and c being constants, or numerical coefficients, and x being an unknown variable. Keep reading for examples of quadratic equations in standard and non-standard forms, as well as a list of quadratic equation terms.
Standard Form Equation Examples
The easiest way to learn quadratic equations is to start in standard form. While not every quadratic equation you see will be in this form, it's still helpful to see examples. Keep in mind that the first constant a cannot be a zero.
Examples of the standard form of a quadratic equation (ax² + bx + c = 0) include:
- 6x² + 11x - 35 = 0
- 2x² - 4x - 2 = 0
- -4x² - 7x +12 = 0
- 20x² -15x - 10 = 0
- x² -x - 3 = 0
- 5x² - 2x - 9 = 0
- 3x² + 4x + 2 = 0
- -x² +6x + 18 = 0
Incomplete Quadratic Equation Examples
As you develop your algebra skills, you'll find that not every quadratic equation is in the standard form. Check out examples of several different instances of non-standard quadratic equations.
Missing the Linear Coefficient
Sometimes a quadratic equation doesn't have the linear coefficient or the bx part of the equation. Examples include:
- 2x² - 64 = 0
- x² - 16 = 0
- 9x² + 49 = 0
- -2x² - 4 = 0
- 4x² + 81 = 0
- -x² - 9 = 0
- 3x² - 36 = 0
- 6x² + 144 = 0
Missing the Constant Term
Quadratic equations can also lack the constant term, or c. For example:
- x² - 7x = 0
- 2x² + 8x = 0
- -x² - 9x = 0
- x² + 2x = 0
- -6x² - 3x = 0
- -5x² + x = 0
- -12x² + 13x = 0
- 11x² - 27x = 0
Quadratic Equation Examples in Factored Form
Factoring is one way to solve a quadratic equation. Here are examples of quadratic equations in factored form:
- (x + 2)(x - 3) = 0 [standard form: x² - 1x - 6 = 0]
- (x + 1)(x + 6) = 0 [standard form: x² + 7x + 6 = 0]
- (x - 6)(x + 1) = 0 [standard form: x² - 5x - 6 = 0]
- -3(x - 4)(2x + 3) = 0 [standard form: -6x² + 15x + 36 = 0]
- (x − 5)(x + 3) = 0 [standard form: x² − 2x − 15 = 0]
- (x - 5)(x + 2) = 0 [standard form: x² - 3x - 10 = 0]
- (x - 4)(x + 2) = 0 [standard form: x² - 2x - 8 = 0]
- (2x+3)(3x - 2) = 0 [standard form: 6x² + 5x - 6]
Examples of Quadratic Equations in Other Forms
Examples of quadratic equations in other forms include:
- x(x - 2) = 4 [upon multiplying and moving the 4, becomes x² - 2x - 4 = 0]
- x(2x + 3) = 12 [upon multiplying and moving the 12, becomes 2x² - 3x - 12 = 0]
- 3x(x + 8) = -2 [upon multiplying and moving the -2, becomes 3x² + 24x + 2 = 0]
- 5x² = 9 - x [moving the 9 and -x to the other side, becomes 5x² + x - 9]
- -6x² = -2 + x [moving the -2 and x to the other side, becomes -6x² - x + 2]
- x² = 27x -14 [moving the -14 and 27x to the other side, becomes x² - 27x + 14]
- x² + 2x = 1 [moving "1" to the other side, becomes x² + 2x - 1 = 0]
- 4x² - 7x = 15 [moving 15 to the other side, becomes 4x² + 7x - 15 = 0]
- -8x² + 3x = -100 [moving -100 to the other side, becomes -8x² + 3x + 100 = 0]
- 25x + 6 = 99 x² [moving 99 x2 to the other side, becomes -99 x² + 25x + 6 = 0]
Quadratic Equation Terms
If you'd like a little more explanation on quadratic equations, check out a list of essential math vocabulary terms. They can help you understand more about quadratic equations, what they're for and how to solve them.
- coefficient - the number that multiplies the variable by a specific amount (the 4 in 4x)
- completing the square - method to solve a quadratic equation in which you divide all terms by the coefficient and add or subtract the constant terms
- constant - a fixed value in an equation
- degree - the largest exponent in an equation; the x2 makes an equation a quadratic equation (or "second degree"), while x3 would make an equation a cubic equation (or "third degree")
- discriminant - the factor in a quadratic equation (b2 - 4ac in the quadratic formula) that indicates if the equation has a real number solution
- factoring - method of solving a quadratic equation by looking for the multiplication factors of the equation
- parabola - a plane curve which is a graphed representation of a quadratic function
- quadratic equation - an equation where the highest exponent of a variable is a square (x2)
- quadratic function - equation expressed as f(x) = a(x - h)2 which is used to graph a parabola
- real number - numbers that have a positive result when multiplied by itself (as opposed to an imaginary number, which has a negative result [√(−1)]
- variable - the letter in a mathematical expression that represents an unknown value (usually what you solve for)
- vertex - the minimum or maximum value of a graphed quadratic function as represented by the point where a parabola changes direction
- quadratic formula - formula used to solve quadratic equations:
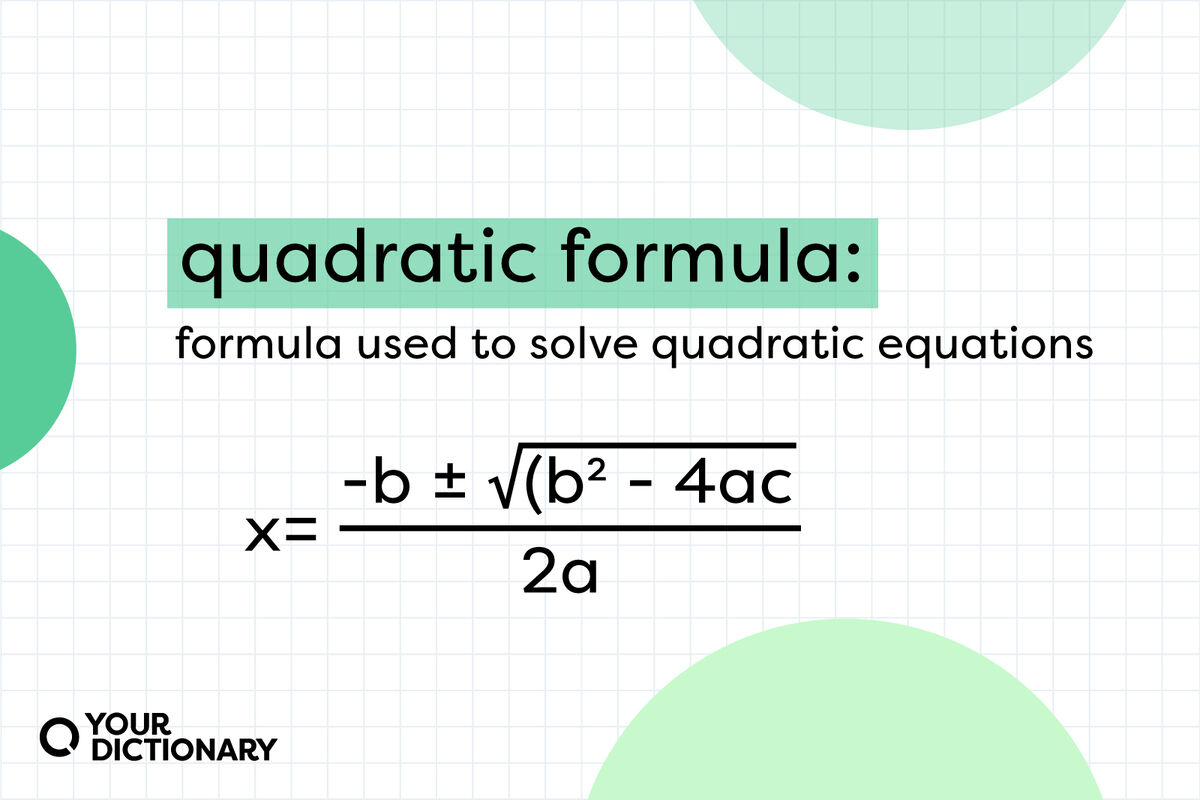
The Logical World of Math
Understanding quadratic equations is a foundational skill for both algebra and geometry. Now that you've seen several examples of quadratic equations, you're well on your way to solving them! Learn more about important math skills with these examples of standard deviation and how it's used in statistics.